It is generally accepted that the Russian mathematician of the 19th century in his theory made parallel lines intersect, contrary to classical, Euclidean geometry. We checked how true this statement is.

In the famous novel by Boris Akunin "Turkish Gambit" one of the heroes says to the other: “Who are you to judge who brings good to civilization and who brings destruction!? He studied the state mechanism and met the leaders! Have you met Count Tolstoy or Fyodor Mikhailovich Dostoevsky? Have you read Russian literature? What, there wasn't enough time? Twice two is always four, and three times three is nine, right? Two parallel lines never intersect? It’s your Euclid that they don’t intersect, but our Lobachevsky’s they do!”

A similar opinion was once expressed by such famous people as writers Alexander Prokhanov, Evgeniy Vodolazkin, Max Fry, journalists Alexey Venediktov And Yulia Latynina, political scientist Leonid Radzikhovsky (although the same Venediktov later will call this particular statement is stupid), head of the Moscow Department of Health Leonid Pechatnikov, as well as less famous figures on the pages TASS, "Izvestia", on Radio Liberty and in many other media.

To begin with, I would like to clarify what the statement about parallel lines from Euclid’s Elements is - the same one that Lobachevsky argued with in his theory. How writes Doctor of Physical and Mathematical Sciences Vladimir Uspensky in his book “Apology for Mathematics,” “almost everyone has heard about the axiom about parallel lines, because they teach it at school.” And the absolute majority of random people he interviewed about its content gave the same clear answer: the axiom is that parallel lines do not intersect.

However, let's look at the source. The first systematic presentation of planimetry (the branch of geometry that studies figures on a plane) was given by the ancient Greek mathematician Euclid in his work "Beginnings". Euclid based his theory on five axioms (or postulates) - statements that do not require proof.

1. From any point to any point you can draw a straight line.

2. A bounded line can be continuously extended along a straight line.

3. A circle can be described from any center by any radius.

4. All right angles are equal to each other.

5. If a straight line intersecting two straight lines forms interior one-sided angles less than two right angles, then, extended indefinitely, these two straight lines will meet on the side where the angles are less than two right angles.

Nothing like the popular formulation, is it? We will turn our attention to the fifth postulate, which in modern sources is often formulated So (a similar idea is attributed to Proclus, and is also sometimes called Playfair’s axiom): “In a plane, through a point not lying on a given line, one and only one line can be drawn parallel to the given one.”

What are parallel lines? By definition (and not at all according to any axiom) these are straight lines that lie in the same plane and do not intersect. Thus, what a huge number of people take as an axiom about parallel lines is just their definition. But the notorious fifth postulate of Euclid looks completely different.

So what did Nikolai Lobachevsky do? For centuries, many of his predecessors tried to prove or disprove Euclid’s fifth postulate, but for this they needed a fulcrum, a base, which could only be this postulate itself. At the same time, at first glance it seems that its truth is obvious. However, the 28-year-old mathematician from Kazan University was not so sure. Lobachevsky tried to replace the fifth postulate with his opposite: “Through a point not lying on a given line, there pass at least two lines that lie in the same plane with the given line and do not intersect it.”

Lobachevsky did not touch the remaining four axioms. Mathematics interested, what will happen after this with the entire system of geometric theorems and other statements, will contradictions emerge that will indirectly prove that Euclid’s assumption, albeit unproven, was the only and inevitably correct one. But it turned out that the world did not collapse. All the basic statements of classical geometry stood up perfectly on this foundation.

It’s just that it’s quite difficult to visually imagine such a situation. Someone will ask: “Why introduce her? It’s important that in theory everything is correct,” and formally he will be right. However, apparently, the members of the scientific commission of Kazan University, who listened to the report of the young mathematician on February 7, 1826, thought differently. Presentation of the work entitled “A condensed presentation of the principles of geometry with a rigorous proof of the parallel theorem” failed, and the manuscript did not even get into print.

Three years will pass, and Nikolai Lobachevsky, now the rector of the university, will find the opportunity to publish his work “On the Principles of Geometry” in the Kazan Bulletin magazine. Unfortunately, the science of that time was not yet ready to accept such an approach - in particular, the work received a negative review Mikhail Ostrogradsky, one of the greatest Russian mathematicians. And only a few years later, Lobachevsky would receive attention in Europe - in particular, the “king of mathematicians” Carl Friedrich Gauss will nominate him as a corresponding member of the Royal Scientific Society of Göttingen, and at the same time will study the ideas of his colleague in the original, in Russian. Gauss himself had held similar ideas, he said, for many years.

And only a decade and a half later, mathematical models will appear in which Lobachevsky’s theory will work without causing endless controversy. In particular, projective model, where the interior of the circle is taken to be a plane, and its chord is taken to be a straight line. As a result, the obvious fact that through one point lying inside a circle one can draw any number of chords that do not intersect with one fixed chord, in such rules of the game becomes an illustration of the fifth law of Lobachevsky geometry. Another example implementation of Lobachevsky's theory - pseudosphere, surface of rotation of a curve:

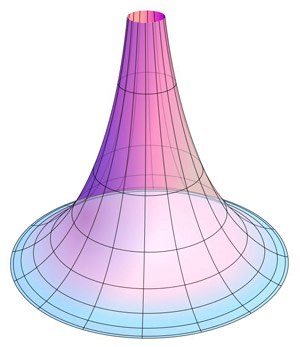
And in 1868 a report will be published Bernhard Riemann, a person who will offer his own approach to non-Euclidean geometry - somewhat different from that of Lobachevsky. However, the success of his theory will be further confirmation of the greatness of the Kazan citizen, since the two mathematicians made similar steps, only in different spaces. Speaking in mathematical terms, then in Euclid Gaussian curvature zero (1), Lobachevsky - negative (2), Riemann - positive (3):

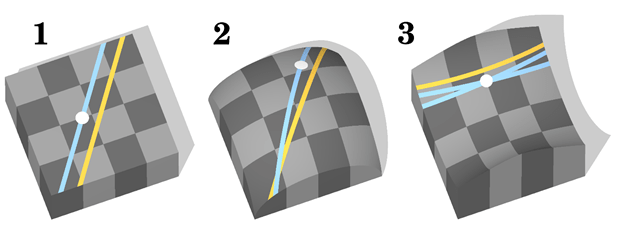
But this is a completely different story, and here it is necessary to conclude that in Lobachevsky’s geometry parallel lines also do not intersect - the Russian mathematician did not claim anything similar. In Riemannian geometry, contrary to the assertions of some Media, Just no parallel lines.